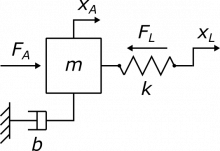
Rigid haptic devices enable humans to physically interact with virtual environments, and the range of impedances that can be safely rendered using these rigid devices is quantified by the Z-Width metric. Series elastic actuators (SEAs) similarly modulate the impedance felt by the human operator when interacting with a robotic device, and, in particular, the robot's perceived stiffness can be controlled by changing the elastic element's equilibrium position. In this research, we explore the K-Width of SEAs, while specifically focusing on how discretization inherent in the computer-control architecture affects the system's passivity. We first propose a hybrid model for a single degree-of-freedom (DoF) SEA based on prior hybrid models for rigid haptic systems. Next, we derive a closed-form bound on the K-Width of SEAs that is a generalization of known constraints for both rigid haptic systems and continuous time SEA models. This bound is first derived under a continuous time approximation, and is then numerically supported with discrete time analysis. Finally, experimental results validate our finding that large pure masses are the most destabilizing operator in human-SEA interactions, and demonstrate the accuracy of our theoretical K-Width bound. Using this work, we can better understand which virtual environments are passive when using SEAs or other compliant haptic devices. As a result, we can improve the safety of these haptic devices during physical human-robot interaction.
To find out more, and see some of our experiments, please go to: